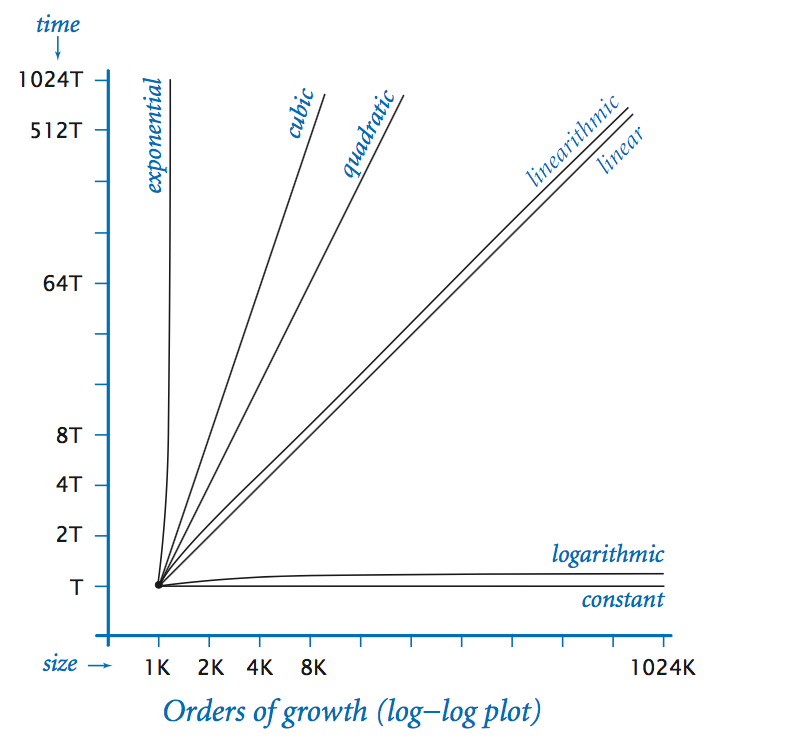
Orders of growth plot
Kotlin provides a standard library called kotlin.system.measureTimeMillis for measuring the time it takes to execute a code block. So running
val time = kotlin.system.measureTimeMillis { /* body of code block */ }time.Kotlin also provides another library called kotlin.system.measureNanoTime that works exactly the same way as kotlin.system.measureTimeMillis except that it returns the running time in nanoseconds.
| description | function | factor for doubling hypothesis |
|---|---|---|
| constant | 1 | 1 |
| logarithmic | log n | 1 |
| linear | n | 2 |
| linearithmic | n log n | 2 |
| quadratic | n2 | 4 |
| cubic | n3 | 8 |
| exponential | 2n | 2n |
