CFG Design

CFG can be regarded as the method of defining strings recursively, which works as follow:
- [basis] give rules for the shortest strings in the language
- [recursion] give rules for constructing longer strings out of shorter ones
For example, let’s try to get rules for the language of balanced parentheses (BP).
1. The shortest string in BP is \(\varepsilon\), so this suggests the rule \(S\to\varepsilon\).
2. Given a string in BP, one can get a longer one by adding ( to its front and adding ) to its end. This suggests the rule \(S\to(S)\).
3. Given two strings in BP, one can get a longer one by concatenating them. This suggests the rule \(S\to SS\).
We now check that all strings in BP can be gotten this way. Consider any string \(w\) in BP. If \(|w| = 0\), then it can be obtained by Rule 1. So assume \(|w| > 0\). Note that \(w\) must start with (, otherwise it can’t be balanced. This initial ( has a unique matching ). This matching closed paren is either at the last position of \(w\) or it is not. If it is, then removing the first and last character of \(w\) leaves a shorter string in BP. Thus \(w\) can be obtained by Rule 2. If it is not, then the prefix of \(w\) ending at this closing paren is in BP, and the remaining suffix of \(w\) is also in BP. Thus \(w\) can be obtained by Rule 3. Everything checks out.

PDA Design

Here is one way:
1. Break the task down into smaller steps.
2. Write pseudocode for each step.
3. Translate the pseudocode into PDA.

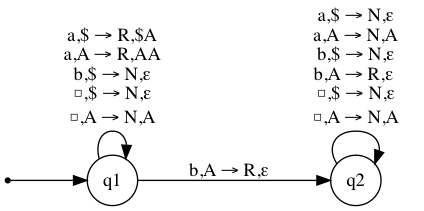
Here is the pseudocode for \(\{ a^nb^n : n \ge 0 \}\).

while a do { read a & push a }
while b do { read b & pop a }
pop $