Playing in a Curvy World

In this project we will experience what it is look to move around in a non-Euclidean environment. The goal of this project is for students to develop an operational and intuitive "feel" for hyperbolic geometry, even before they have proven any of its properties.

1. In Geometry Explorer one can open up a Hyperbolic window by using the File menu and choosing "Hyperbolic" when the Open dialog box appears.  A new window will pop up with a circular disk inside.  This disk is called the "Poincare Disk" in honor of Henri Poincare, one of the greatest mathematicians of the 20th century.  You should think of this disk as a little "geometric universe", just as you think of the plane as a universe to do normal geometry.  This disk is a model for a geometry called Hyperbolic Geometry.  In this project we will explore what it is like to "live" in this strange geometric universe. That is, what is similar to living in a Euclidean universe and what is different.

2.  In the first part of this project we will look at triangles in the Poincare disk.  In the Hyperbolic window below we have created a triangle ABC  and measured its interior angles.  Using the Calculator we have found the sum of the interior angles of triangle ABC.

Note that the sum of the angles is not 180 degrees, as in Euclidean Geometry. In fact, the angle sum is less than 180 degrees. In the first part of this lab I want you to speculate on the behavior of triangles in hyperbolic space. Without doing anything on the computer think about and then write down what you think will happen in the following situations:

1) The three vertices of the triangle approach the boundary circle.
2) The three vertices of the triangle shrink down to almost a single point.

Now, carry out some experiments in the window above by dragging the vertices of the triangle around and record the results. Are your conjectures verified?  Hyperbolic geometry is often called "locally" Euclidean. What do you think this means in terms of the experiments above?

3. In the second part of this project we will investigate another very strange property of hyperbolic geometry having to do with moving about in the geometry.  Here we have used the circle and segment tools to construct a hyper-person.

4.  Use the select tool to draw a box around the person, thus selecting all the objects making up the figure.  Then, hold the shift key down and drag the person in a circle and return to your original spot.  You will notice that our little being does cartwheels as you drag him/her around the disk.  Also, when you return back to where you started the figure will not be in the original position!!  Shown below is one result of doing this.

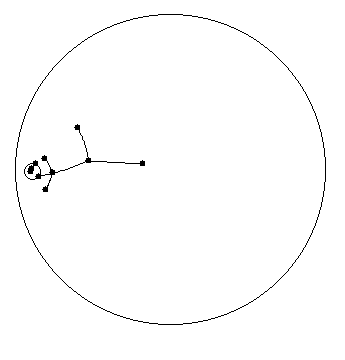
Now, you may think that our hyper-being has also changed size as we moved around the disk. But, he is actually always the same size!  Note that measurements of the lengths and circumferences that make up the figure remain constant as we move around.

5. The property of changing orientation as you move around is generally true of spaces that are "curved".  By this we mean that the space is not flat like Euclidean space is.  In a flat space if we just walk around in a circle and return to where we started, we always end up in the same position.  But, this does not happen in a curved space, like Hyperbolic Space.

6. What other differences can you discover between Hyperbolic and Euclidean Geometry?  Are there parallel lines? perpendicular lines? Does the Pythagorean Theorem hold true?  Experiment with this Geometry and find two things (other than the two illustrated above) that are different between Hyperbolic and Euclidean geometry.

7. As Janos Bolyai (one of the discoverers of non-Euclidean geometry) said "I have discovered such wonderful things that I was amazed ... out of nothing I have created a strange new universe."  Hyperbolic geometry is indeed a very weird place.  However, it has proven to be a very useful geometry for modern theories of the geometry of the universe.  Extra Credit: Research the idea that the universe may be curved.  Write-up a short report of your findings.