Transposition

The twenty-six puzzles in this collection all have the same goal: By sliding blocks into open spaces on the board, exchange the positions of the two colored blocks. As an example, here is the "Medium 7" puzzle:

Start Playing!

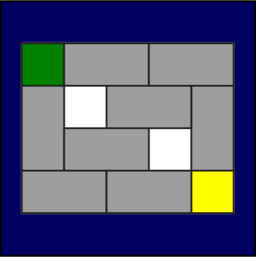
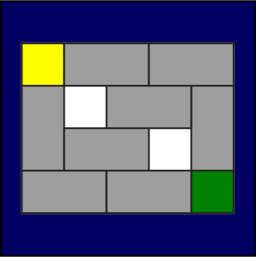
Note: You've solved the puzzle as soon as the colored blocks have been swapped. In almost all of the puzzles, you can swap the colored blocks and restore all of the gray obstacles to their original position as well: a “Perfect Solve,” as in the example above. You may attempt the Perfect Solve as a further challenge once you have achieved the basic swap, but beware: there is one puzzle where it is not possible.

Generating The Puzzle Pool

I enjoy sliding block puzzles, but the “Move Block A to Position X” type of puzzle feels arbitrary. Transposition puzzles seem a little more natural and satisfying. And especially when the goal of the puzzle is a transposition, it's aesthetically pleasing if the layout has some symmetry as well.

So: In creating this collection, I began by enumerating all symmetric arrangements of blocks that are possible on 4x3, 4x4, and 5x4 grids (subject to a few constraints for making reasonable puzzles, for example, enough blank space for all the pieces to move). The rectangular boards allow horizontal and vertical reflections, as well as 180- and (in the 4x4 case) 90-degree rotations.

From these, I selected layouts with a “distinguished pair” of blocks — two blocks of different shape from all the others in the puzzle, which would be the target pieces to swap. At this point I had a pool of 13,961 different board layouts which potentially represented good transposition puzzles, but many of them would not be solvable, and of course many of them were rearrangements of one another — different states of the same puzzle. Unsurprisingly, the 5x4 layouts were the vast majority of those (12,573 of them).

Figure 1: 1,194 symmetric 4x4 layouts

Next, I gathered all of the layouts into equivalence classes, determining which layouts were related to each other by legal sliding moves (different states of the same puzzle), and tested them for their solvability. The gathering and solvability-testing took place together. If any one layout in the class was Perfectly Solvable then I knew that every other layout in that class was Perfectly Solvable as well. But if no Perfectly Solvable layout had been found in a particular class yet, then each new layout in that class had to be thoroughly explored to see if it admitted any solution at all (“Weakly Solvable”).

Figure 2: Gathering and Testing. This is a representation of a small sample of the data at this point. Layouts in the same row of the table are equivalent to each other by sliding, and the solvability status of each layout is identified.

Making a Selection

One of my summer goals was to submit a nice collection of sliding block puzzles to the Wolfram Demonstrations Project. I had already chosen some “classic” puzzles from Hordern's book, and some puzzles of my own design where the goal is to join like-colored blocks together. I wanted to round out the collection with well-chosen transposition problems.

Link: Sliding Block Puzzles [Wolfram Demonstrations]

The choice of problems to include was computer-assisted, but ultimately came down to my own judgment (hence, some arbitrary decisions). First, I set a target number of puzzles to include. To limit the pool, I identified within each class the transposition puzzle with the longest solution as a representative for that class. I sorted those representatives according to solution length, and then just inspected the puzzles by hand. I tried to spread the selection out over all the different solution lengths, to choose puzzles that looked visually attractive, and to include puzzles with a variety of different block shapes to be transposed (unit blocks, vertical and horizontal dominoes, and 2x2 blocks).

I also weeded out puzzles with long solutions (as measured by the number of the slides) that were simply tedious, as opposed to puzzling in an interesting way. This tends to happen when there is a large number of small blocks. “Medium 4” is a case in point — I included it in order to have a puzzle with 2x2 blocks to swap, but it's far easier than its solution length suggests. This is where the element of human judgment was critical.

I thought a lot about ways to algorithmically distinguish between interesting long solutions and dull ones, tried a lot of metrics, and ultimately didn't find a good solution. Hand-selection gave the best results... and there's something satisfying about being the curator of a collection, in any case. But I'm still interested in finding computational ways to judge the difficulty of a puzzle in a way that corresponds with human perception.

The Chosen Puzzles

The table below shows each puzzle together with the minimum number of slides required to solve the puzzle. The number given is just for swapping the colored blocks; I haven't included the minimum number for a Perfect Solve. The solution lengths were computed with JimSlide. The “Very Hard 4” puzzle doesn't quite belong with the rest, as its layout isn't strictly symmetrical in the same way that the others are. Think of it as a hand-crafted bonus, and probably the most challenging of the lot.

External Links

Many old web pages with sliding block puzzles no longer work due to changes in browser technology. If you want to read and play more, here is a short list of good starting places:

1. Solving Rush Hour, the Puzzle

   Michael Fogleman's page on creating a database of interesting 6x6 Rush Hour puzzles directly inspired the presentation of this page. It's a great read, you can study his code, and the puzzles are (frustrating) fun to play, too.

2. Sliding Block Puzzles, Part 3 and Part 4

   Neil Bickford's pages describe the search for puzzles on the 4x4 grid with long solutions — another enjoyable read. Part 3 includes a generous collection of references and links.

3. Sliding Block Puzzle Solver

   You can use it to find solutions to all the transposition puzzles on this page, if you're stumped. It does have some quirks in puzzles with non-convex pieces.

4. The Nondeterministic Constraint Logic Model of Computation: Reductions and Applications

   (Robert A. Hearn and Erik D. Demaine). This 12-page paper gives complexity results for sliding block puzzles like these, as well as Rush Hour and sokoban-type puzzles, by showing how such puzzles can encode gates and circuits with computational power equivalent to a Turing machine.