Three in a row project

For this lab, you will be using backtracking to solve a common puzzle problem. For a more complete description of these puzzles, please visit This site

Simple introduction

Your code will take a file specifying an n-by-n grid which represents an initial state for a three-in-a-row game. The format of the file will have the first line contain the value for n followed by n lines of n colors each, such as

6
B---B-
W--B-W
------
WW--B-
------
--W---

Which has a graphical representation of:

The basic rules to solve these are:

All squares must be filled in either white or blue.
All rows and columns must have an equal number of whites and blues.
There may be not be an serires of three consecutive blue or whites.

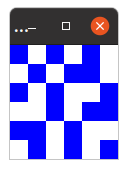
A solution to this problem would be

  
BWBWBW
WBWBBW
BWBWWB
WWBWBB
BBWBWW
WBWBWB

Which has a graphical representation of:

What you will be given

There are three python files for this lab:

threeInARowBoard.py, the python file which specifies a board class to hold the board.

threeInARowBoard.html, HTML file documenting the board class.

threeInARowMain.py, which start the game.

threeInARowSolver.py, which you will complete to make it work. And additional support files:

03-26-easy-6x6.in, an easy 6x6 board.

2018-03-30-medium-6x6.in, a medium 6x6 board.

2018-03-30-medium-14x14.in, a medium 6x6 board.

allBlankSix.in, a blank 6x6 board.

allBlank14.in, a blank 14x14 board.

The algorithm to complete the game

Your code will use the following algorithm to complete the game.

Find the next '-' or undefined location

Have you reached the end of the board without finding one? If so, return whether or not it is a solution.
If you found one do the following:
- Place one color at that location, typically blue is tried first,
  - First check to make sure row and column are valid to speed things along.
  - Then recursively see if the board can be solved.
- If you found a solution with that color in that location, return True.
- If the board cannot be solved with that color in that location, place the other color in that location.
  - First check to make sure row and column are valid to speed things along.
  - then recursively see if the board can be solved.
- If you found a solution with that color in that location, return True.
- If the board cannot be solved with either color in that location, reset the value at that location to '-' and return False.

Following this algorithm, you will have one of two outcomes. Hopefully, you will have have found a valid solution, stopping as soon as you do. If not, you will have exhausted all possibilities and shown that a solution does not exist, ultimately returning False.

What you need to do

Ultimately, you need to complete the function findSolution(board) in the file threeInARowSolver.py This quite likely will be best done writing additional helper functions as well. Think about some of the additional things that will need to be done, such as the following:

How are you going to check if a row or column is initially viable? IE, does it already have too many tiles that are blue or white? Does it have too many consective tiles that are blue or white?
How are you going to check the entire board? When should you do this?
Any other tasks that you think should be a function, make it a function. In general, if you ever think 'I wish there was a function to do X, write one. Sometimes that function will already exist in Python.

You will need to download the files listed again here:

threeInARowBoard.py, the python file which specifies a board class to hold the board.

threeInARowMain.py, which start the game.

threeInARowSolver.py, which you will complete to make it work.

03-26-easy-6x6.in, an easy 6x6 board.

2018-03-30-medium-6x6.in, a medium 6x6 board.

When you run the file, it will ask you to choose a file. The file you choose should be one of the initial boards listed above, such as 03-26-easy-6x6.in.

I have created short video going over a solution of this in action. This is a backtracking specific video going over the backtracking method for solving the 3-in-row problem. This is longer and may be a little too pedantic. And now one video going over how we would solving the 3-in-row problem when not using a computer.