Deterministic Finite Automaton (DFA)

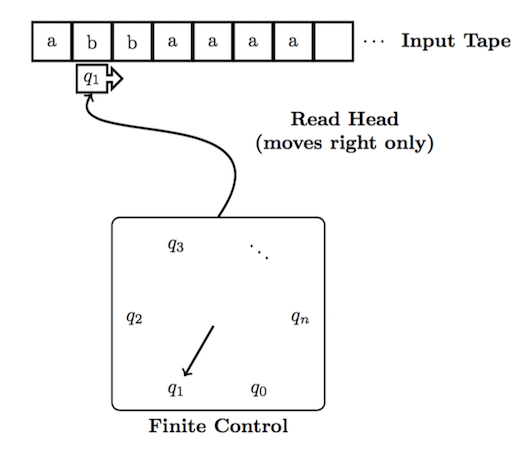
• A DFA is a machine with

  • an input tape divided into cells; each cell contains exactly one symbol
  • a read head that’s positioned on exactly one cell at any point in time
  • a finite control consisting of a set of possible states the machine can be in
  • a program called transition table where, given any state and any symbol, the program specifies the next state to transition to

DFA Anatomy

DFA Computation

• Input string is given on the tape, one symbol per cell.

• Machine starts in a default start state with its read head positioned at the start of tape.

• In each computation step, the machine uses its current state and the symbol under its read head to determine which next state to transition to. It then transitions to the next state and moves right one cell.

• Machine knows when it is at the end of input.

• Some states are marked as special.

• Input string is accepted iff the machine ends up in a special state.

Formal Definition

• A DFA \(M\) is a 5-tuple \((Q, \Sigma, \delta, q_0, F)\), where

  • \(Q\) is a finite set of states
  • \(\Sigma\) is an alphabet
  • \(\delta : Q\times\Sigma\to Q\) is a transition function
  • \(q_0\in Q\) is the start state
  • \(F\subseteq Q\) is the set of accept (or accepting, or final) states

DFA Diagram

• A state/transition diagram is a (multi)digraph that depicts a DFA.

  • Vertices represent states.
  • Edges correspond to state transitions.
  • Each edge is labelled by the symbol that causes that transition.
  • Start state has an arrow from nowhere pointing into it.
  • Final states are doubly circled.
  • A string \(w\) of length \(n\) is accepted by the DFA iff there exists a directed path that begins at the start state and ends in some final state such that the sequence of labels on the edges of the path is \(w_1, w_2, \ldots, w_n\).

DFA Example

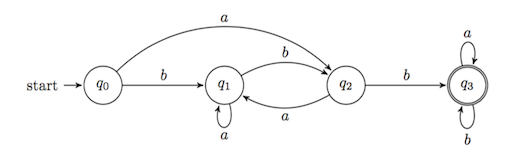
• This diagram represents the DFA \(M=(Q, \Sigma, \delta, q_0, F)\), where

  • \(Q = \{ q_0, q_1, q_2, q_3 \}\)
  • \(\Sigma = \{ a, b \}\)
  • \(\delta\) is given by the following table
    
    
  • \(q_0\) is the start state
    
  • \(F = \{ q_3 \}\)

Acceptance by DFA

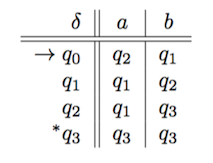
• A string \(w\in \Sigma^*\) of length \(n\) is accepted by DFA \(M\) iff there exists a sequence of states \(r_0, r_1, \ldots, r_n\) such that

  • \(r_0=q_0\)
  • \(r_n \in F\)
  • \(\delta(r_{i-1}, w_i) = r_i\) for \(i=1,2,\dots,n\)

• \(L(M)\), the language recognized by \(M\), is the set of all strings accepted by \(M\), i.e., \(L(M) = \{ w\in\Sigma^* : M \text{ accepts } w \}\).

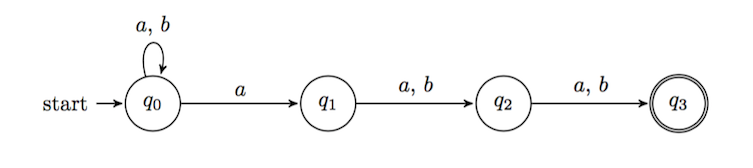
• Exercise. Show that \(ab\) and \(babb\) are accepted by this machine but \(aab\) and \(bbaa\) are not.
  

Remarks

• We use comma-separated list of symbols as a shorthand for parallel edges, each labelled by a symbol in the list.
  

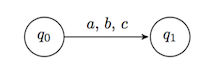
• We may even use ellipsis for understood omitted symbols.
  

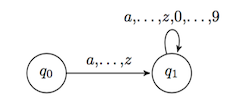
• Sipser also uses \(\Sigma\) to represent a list of all symbols from the alphabet.

Nondeterministic Finite Automaton (NFA)

• An NFA differs slightly from a DFA in its program and how it computes.

• Given the current state and the symbol under the read head, an NFA has a number of (possibly zero) states that it can transition to.

• Moreover, in some specific states an NFA may change its current state without moving its read head.

• A DFA computation is always successful; it either ends up in an accepting or non-accepting state. In contrast, an NFA computation can crash! This occurs when the machine is in a state and reading a symbol such that its program has no transition for that combination of state & symbol. Moreover, an NFA computation can get into an infinite loop. (How?)

• A string is accepted by an NFA M if it has an accepting computation by M.

Formal Definition

• A nondeterministic finite automaton (NFA) \(M\) is a 5-tuple \((Q, \Sigma, \delta, q_0, F)\), where

  • \(Q\) is a finite set of states,
  • \(\Sigma\) is an alphabet,
  • \(\delta : Q\times(\Sigma\cup\{\varepsilon\})\to 2^Q\) is the transition function,
  • \(q_0\in Q\) is the start state, and
  • \(F\subseteq Q\) is the set of accept (or accepting or final) states.

Acceptance by NFA

• A string \(w\in \Sigma^*\) of length \(n\) is accepted by \(M\) if and only if we can write \(w=y_1y_2\dots y_m\), where each \(y_i=\varepsilon\) or \(y_i\in\Sigma\), and there exists a sequence of states \(r_0, r_1, \ldots, r_m\) such that

  • \(r_0=q_0\)
  • \(r_m \in F\)
  • \(r_i\in \delta(r_{i-1}, y_i)\) for \(i=1,2,\dots,m\)

• The set of all strings accepted by \(M\) is the language \(L(M)\) recognized by \(M\), i.e., \(L(M) = \{ w\in\Sigma^* : M \text{ accepts } w \}\).

• Note that \(m\ne n\) is possible. (Why?)

Remarks

1. In a state/transition diagram for a DFA where \(\Sigma\) has \(n\) symbols, every state has exactly \(n\) edges leaving it, one edge per symbol in \(\Sigma\). In a state/transition diagram for an NFA, on the other hand, some state may have more or fewer than \(n\) edges leaving it. Moreover, two distinct edges leaving the same state may have the same label, and some edge may be labelled with \(\varepsilon\).

2. If a string \(w\) is accepted by a DFA, then there exists a unique path from the start state to a final state that traces out \(w\). On the other hand, if a string \(w\) is accepted by an NFA, then there exists at least one path (may be more) from the start state to some final state that traces out \(w\).

NFA Example

• Let \(L_3\) be the language of all strings over \(\Sigma = \{a, b\}\) whose 3rd symbol from the right end is \(a\). Here is an NFA recognizing \(L_3\).
  

• A DFA recognizing \(L_3\) will have to memorize the last 3 symbols seen, i.e., it needs \(2^3\) states (in general, \(|\Sigma|^3\) states).

• Exercise. Design a DFA that recognizes \(L_3\).