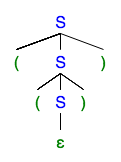
Parse Trees
A parse tree is a rooted, ordered, node-labeled tree with these properties.
- The root node is labeled with the start variable.
- Every internal node is labeled with a variable.
- Every leaf node is labeled with a terminal or \(\varepsilon\).
- For any internal node, say one with label \(A\), if the labels of its children are read from left to right, then we’ll get a string, say \(\alpha\), such that \(A\to\alpha\) is a grammar rule.
The yield of a parse tree is the string obtained from concatenating the labels of all its leaves from left to right.
Using the grammar of the language of balanced parentheses, we get the string
(())as the yield of this parse tree