Growth of functions
Table from Gary & Johnson’s Computer and Intractability A Guide to the Theory of NP-Completeness
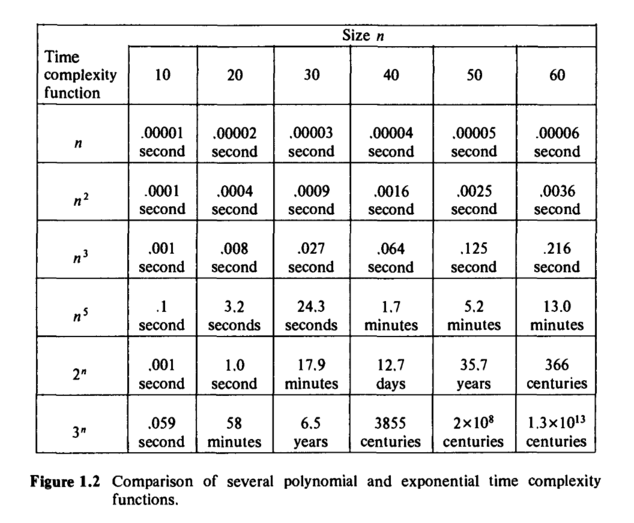
Table from Gary & Johnson’s Computer and Intractability A Guide to the Theory of NP-Completeness

\(PATH\) can be solved by this algorithm.
M = "On input <G,s,t> where G is a directed graph, s and t are vertices:
mark s;
while (there exists some edge, say uv, with u marked and v not marked) do {
if (v = t) accept;
else mark v;
}
reject;"This algorithm then takes time \(O(n^2)\) on the RAM. So \(PATH\) is in \(\mathcal{P}\).
\(RELPRIME\) can be solved by this algorithm.
M = "On input <x, y> where x and y are nonnegative integers:
while (y != 0) do {
(x, y) := (y, x mod y);
}
if (x = 1) accept;
else reject;"On the RAM this algorithm takes \(O(n)\) time where \(n\) is the number of bits used to represent the maximum of \(x\) and \(y\).