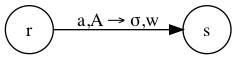Pushdown Automata
San Skulrattanakulchai
March 14, 2019
Deterministic Pushdown Automaton (DPDA)
- A DPDA has an input tape divided into cells. Each cell may have a symbol from the tape alphabet \(\Sigma\) written on it, or be empty, which we denote by the blank symbol \(\square\) that is not a tape symbol.
- There’s a tape head that is at any given moment scanning some cell, and can read the symbol on the cell it is currently scanning.
- There’s a stack that at any given moment may contain a collection of symbols selected from the stack alphabet \(\Gamma\). The stack alphabet contains a special symbol $ that will automatically be placed as the only symbol on the stack when the DPDA starts.
- There’s a stack head that can read the top symbol of the stack. The stack is equipped with a mechanisam to have its top symbol popped off, then followed by having a string of zero or more stack symbols being pushed onto it.
- There’s a non-empty, finite set of states \(Q\), one of which is designated as the start state.
DPDA Computation
- The machine starts out in the start state with its stack containing only $, and the input string written on the tape, one symbol per cell, and the tape head positioned at the start of tape.
- In each computation step, the machine inspects its current state and the symbol currently being scanned. It then performs all these three things as specified by the transition function:
- it stays in its old state or changes to a new state
- it remains stationary or moves the read head right one cell
- it pops the top symbol off the stack, then pushes a string of zero or more stack symbols onto the stack
- The machine terminates as soon as the stack becomes empty.
Acceptance/rejection
- We say that the machine accepts an input string \(w\) iff the machine starts its computation with \(w\) on its tape and terminates when the head is one cell to the right of the last input symbol.
- We say that the machine rejects an input string \(w\) iff the machine starts its computation with \(w\) on its tape and it never terminates, i.e. it loops forever, or it terminates but at the time of its termination, the tape head is not on the cell immediately to the right of the cell containing the last symbol of the input string.
DPDA Transition diagram
- We can represent a DPDA as a multi-digraph diagram similar to a DFA.
- The vertices represent states.
- The start state has an arrow pointing into it from nowhere.
- Each transition \(\delta(r, a, A) = (s, \sigma, w)\) is represented by a directed edge from state \(r\) to state \(s\) labeled \(a, A \to \sigma, w\).
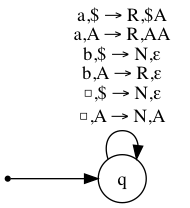
Example DPDA (transition diagram)
- Here is the transition diagram for the DPDA for the language of “balanced parentheses”.
Nondeterministic Pushdown Automaton (NPDA)
- An NPDA \(M\) is a 5-tuple \((\Sigma, \Gamma, Q, \delta, q)\), where the working of the machine is defined in exactly the same way as a DPDA, except for the transition function.
- For an NPDA the transition function is a a function \(\delta : Q\times(\Sigma\cup\{\square\})\times\Gamma \to 2^{Q\times\{N, R\}\times\Gamma^*}\), i.e., the current computation step may not be uniquely defined, but the automaton can make a choice out of a finite number of possibilities.
- Acceptance of an input string \(w\) by an NPDA is defined to be an existence of an accepting computation, in which the machine can choose to execute any of the possible choices it has available to it at each step.
- Rejection of the input string \(w\) is defined to be such that every possible computation of \(w\) is rejecting or crashing. (Note that an NPDA computation can crash!)
- The language \(L(M)\) of the NPDA \(M\) is defined to be the set of all strings over \(\Sigma\) that are accepted by \(M\), just like in the case of a DPDA.
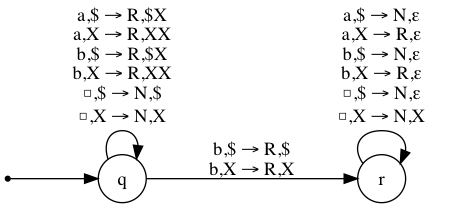
Example NPDA (transition diagram)
- Here is the transition diagram for the NPDA for the same language \(\{ wbv : w,v \in\{a,b\}^*, |w| = |v| \}\).