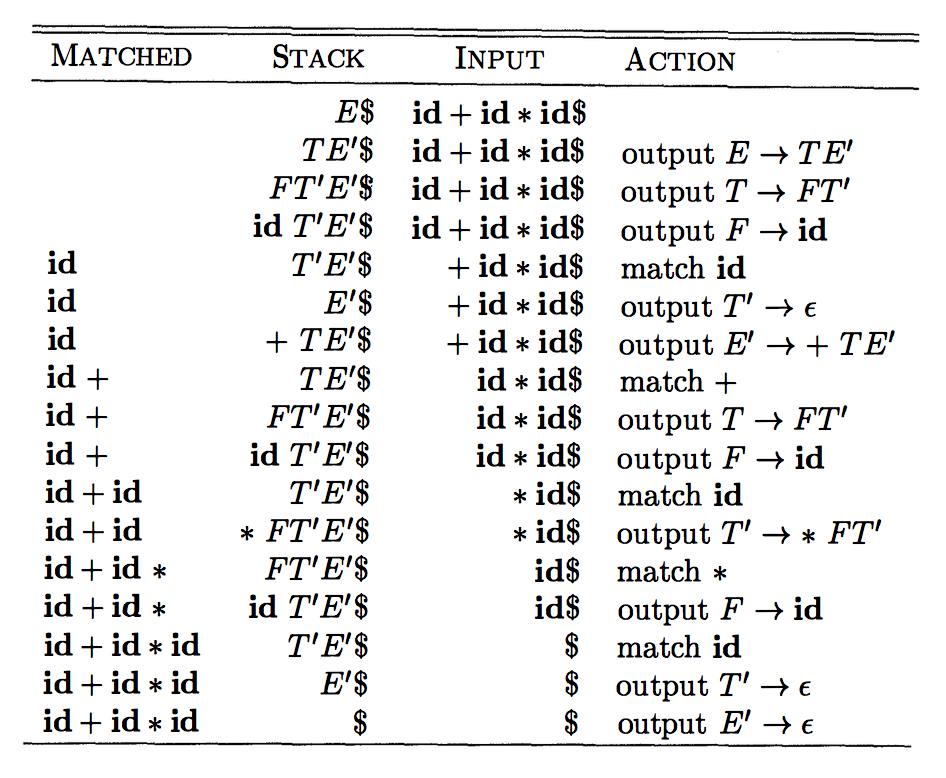
An example LL(1) grammar
Verify that this grammar
E → T E' E' → + T E' | ε T → F T' T' → * F T' | ε F → ( E ) | idis in LL(1) and it has this \(M\) table
For each nonterminal \(A\), we write a recursive procedure A() with this outline:
A() {
choose an A-production A → X1 X2 ... Xk;
for i ← 1 to k do {
if Xi is a nonterminal then
Xi();
else if Xi = current input symbol then
advance input to the next symbol;
else
error();
}
}The “choose an A-production …” step needs to be tried for all possible A-production in a backtracking manner. This requires updating/downdating the input pointer for every backtracking step as well.
Here is an algorithm for computing the set \(N(G)\).
Q ← empty queue;
NG ← empty set;
for all A ∈ V do {
if A → ε then {
NG ← NG ∪ {A};
enqueue(A, Q);
}
}
while Q is not empty do {
A ← dequeue(Q);
mark all occurrences of A in all productions;
if this marking of A results in all Xi (1 ≤ i ≤ k)
of any production B → X1 X2 ... Xk being marked
but B itself is unmarked then {
NG ← NG ∪ {B};
enqueue(B, Q);
}
}
return NG;FIRST setsFIRST and FOLLOW, that are helpful for constructing both the top-down and the bottom-up parsers.first\((\alpha)\) to be \[
\mbox{first}(\alpha) := \{a\in\Sigma : \alpha \Rightarrow^* a\beta
\text{ for some string of grammar symbols }\beta\}.
\] Note that first\((a) = \{a\}\) for all \(a\in\Sigma\).FIRST\((\alpha)\) is defined to beFIRST\((a)\) = first\((a) = \{a\}\) for all \(a\in\Sigma\). Also, FIRST\((\epsilon) = \{\epsilon\}\) since first\((\epsilon) = \emptyset\) and \(\epsilon\) is nullable.FIRST setsFIRST(\(a\)) = first(\(a\)) = \(\{a\}\) for all \(a\in\Sigma\).FIRST sets of all nonterminals by following these three steps:
first(\(\alpha\)) for all nonempty alternatives \(\alpha_i\) (\(1\le i\le n\)) of the \(A\)-productions \(A\to \alpha_1 \mid \alpha_2 \mid \cdots \mid \alpha_n\). The set first(\(A\)) is simply \(\bigcup_{i=1}^n\) first(\(\alpha_i\)). Details of this step will be given on next slide.FIRST(\(A\)) from first(\(A\)) and the nullability or non-nullability of \(A\) using the definition of FIRST.Once we know first(\(A\)) (and thus FIRST(\(A\))) of all nonterminals \(A\), we can compute first(\(\alpha\)) (and thus FIRST(\(\alpha\))) of any nonempty string of grammar symbols \(\alpha\). The algorithm is as follows:
Let α = X1 X2 ... Xn;
first_α ← ∅;
for i ← 1 to n do {
first_α ← first_α ∪ first(Xi);
if Xi is not nullable then
return first_α;
}
return first_α;first sets of all nonterminalsHere is my algorithm for computing first(\(A\)) for all nonterminals \(A\).
for each nonterminal A ∈ V do
initialize first(A) to be empty set;
Let H be a digraph whose vertex set is V and empty edge set;
for each nonterminal A ∈ V do {
for each non-ε-production of A, say, A → X1 X2 ... Xn, do {
for i ← 1 to n do {
if Xi is a terminal then
first(A) ← first(A) ∪ { Xi };
else
add a directed edge (Xi,A) to H;
if Xi is not nullable then break;
}
}
}
/* This step contracts all strong components of H. */
while H contains a directed cycle C do {
contract C to a supervertex and set the first set of
this supervertex to be equal to the union of first(v)'s
for all vertices v on C;
}
/* At this point H is a dag! */
topologically sort H;
for each vertex v in H in topological order do {
for each edge (v,w) do {
first(w) ← first(w) ∪ first(v);
}
}FIRST setsGiven the Grammar
E → T E'
E' → + T E' | ε
T → F T'
T' → * F T' | ε
F → ( E ) | idrun the algorithm to verify that
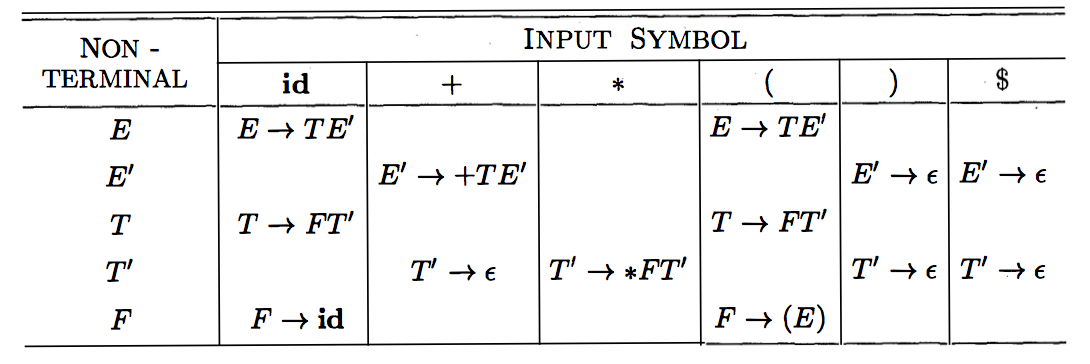
FIRST(T) = FIRST(F) = FIRST(E) = { (, id }
FIRST(E') = { +, ε }
FIRST(T') = { *, ε }FOLLOW setsfollow(A) is defined to be \[
\mbox{follow}(A) := \{ a\in\Sigma : S\Rightarrow^*
\alpha Aa\beta \mbox{ for some strings of grammar symbols }
\alpha, \beta \}.
\]FOLLOW(\(A\)) is defined to be \[
\mbox{FOLLOW}(A) :=
\left\{
\begin{array}{ll}
\mbox{follow}(A)\cup\{\$\},
& \mbox{if $S\Rightarrow^* \alpha A$ for some string of grammar symbols
$\alpha$} \\
\mbox{follow}(A), & \mbox{otherwise.}
\end{array}
\right.
\] Note that \(\$\in\) FOLLOW(\(S\)) always.FOLLOW sets for terminals using exactly this same definition. We are focusing on the FOLLOW sets of nonterminals only because they are needed for parsers.FOLLOW sets of all nonterminalsHere is my algorithm for computing FOLLOW(\(A\)) for all nonterminals \(A\).
for each nonterminal A ∈ V do
initialize FOLLOW(A) to be empty set;
FOLLOW(S) ← { $ };
Let H be a digraph whose vertex set is V and empty edge set;
for each nonterminal A ∈ V do {
for each non-ε-production of A, say, A → X1 X2 ... Xn, do {
for i ← n downto 1 do {
if Xi is a nonterminal then {
Let β be the string X{i+1} X{i+2} ... Xn;
FOLLOW(Xi) ← FOLLOW(Xi) ∪ first(β);
if β is nullable and A ≠ Xi then
add a directed edge (A, Xi) to H;
}
}
}
}
/* This step contracts all strong components of H. */
while H contains a directed cycle C do {
contract C to a supervertex and set the FOLLOW set of
this supervertex to be equal to the union of FOLLOW(v)'s
for all vertices v on C;
}
/* At this point H is a dag! */
topologically sort H;
for each vertex v in H in topological order do {
for each edge (v,w) do {
FOLLOW(w) ← FOLLOW(w) ∪ FOLLOW(v);
}
}FOLLOW setsGiven the Grammar
E → T E'
E' → + T E' | ε
T → F T'
T' → * F T' | ε
F → ( E ) | idrun the algorithm to verify that
FOLLOW(E) = FOLLOW(E') = { ), $ }
FOLLOW(T) = FOLLOW(T') = { +, ), $ }
FOLLOW(F) = { +, *, ), $ }FIRST and FOLLOW sets into a 2D array \(M[\cdot,\cdot]\) such that for any \(A\in V\) and for any \(a\in\Sigma\cup\{\$\}\), the value \(M[A,a]\) gives the production to apply when the parser tries to expand a node \(A\) when the lookahead symbol is \(a\).Algorithm:
for each production A → α do {
for each terminal a in first(α) do
M[A,a] ← M[A,a] ∪ { A → α };
if α ⇒* ε then {
for all a ∈ FOLLOW(A) do
M[A,a] ← M[A,a] ∪ { A → α };
}
}Any table entry \(M[A,a]\) that remains empty after the algorithm finishes signifies ERROR for the parser, i.e., if the parser using this table is trying to predict which production to apply at node \(A\) while the lookahead symbol is \(a\), the parser knows that the input is invalid, so it can abort.
Verify that this grammar
E → T E'
E' → + T E' | ε
T → F T'
T' → * F T' | ε
F → ( E ) | idis in LL(1) and it has this \(M\) table

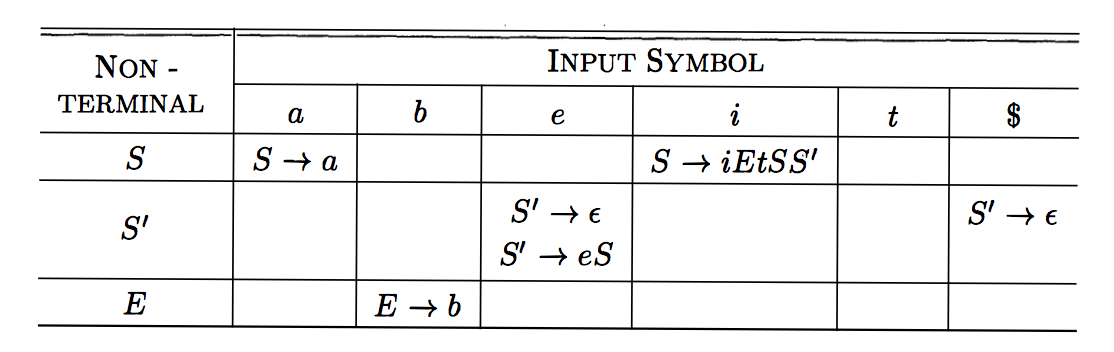
Verify that this grammar
S → i E t S S' | a
S' → e S | ε
E → bis not in LL(1) and it has this \(M\) table
Algorithm:
a ← first input symbol;
X ← top stack symbol;
while X ≠ $ do {
if X = a then {
pop the stack;
a ← next input symbol;
} else if X is a terminal then error();
else if M[X,a] is empty then error();
else {
let M[X,a] be X → Y1 Y2 ... Yk;
output the production M[X,a];
pop the stack;
for i ← k downto 1 do
push Yi on the stack;
}
X ← top stack symbol;
}Execution of the non-recursive predictive parsing algorithm for the grammar
E → T E'
E' → + T E' | ε
T → F T'
T' → * F T' | ε
F → ( E ) | idon the input string id + id * id is depicted here: