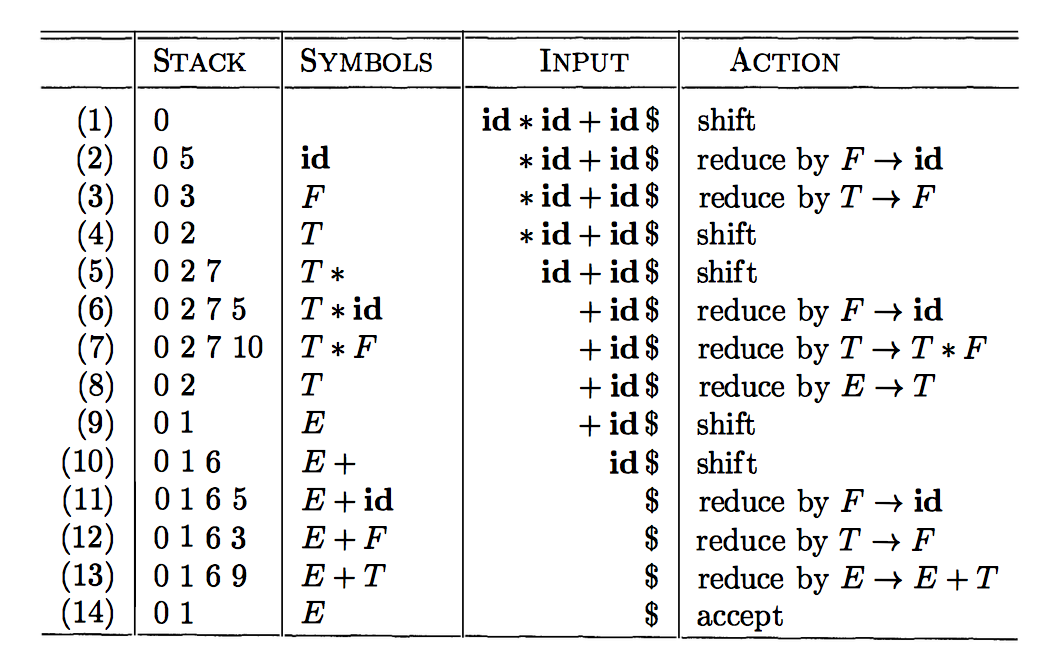
Example LR(0) automaton
An LR(0) item (or simply item) is a production with a mark in it. A production \(A \to X_1X_2\cdots X_n\) with length-\(n\) body can give rise to \(n+1\) items. E.g., production \(A\to\epsilon\) gives item \([A\to ●]\) and production \(A\to aXY\) gives these four items
[A → ●aXY]
[A → a●XY]
[A → aX●Y]
[A → aXY●]Each item represents a state of the parser. For example, an item like [A → aX●Y] represents the state where the parser has already seen an input string derivable from aX and is hoping to see a string derivable from Y next. An item like [A → aXY●] represents the state where the parser has already seen the whole body aXY and perhaps it’s time to reduce it to A.
# LR(0) automaton
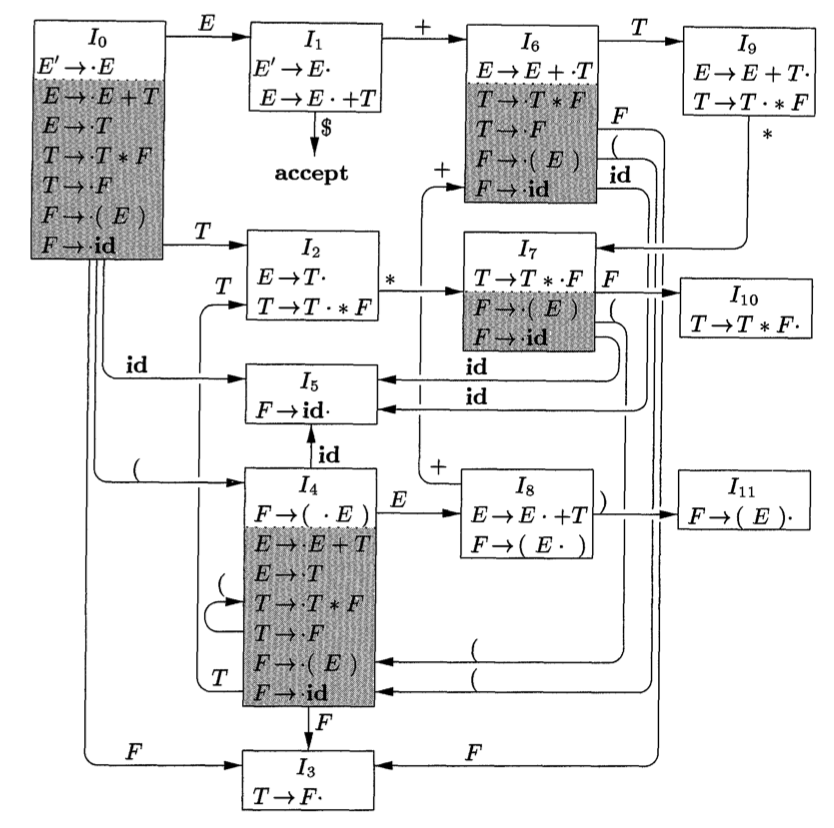
The resulting DFA is the one described in the dragon book as the LR(0) automaton. Each state of the DFA is a set of LR(0) items. Its collection of states is called the canonical LR(0) collection. They also use the convention of deleting the dead state (or trap state) from the picture.

CLOSURE(I) and GOTO(I,X) functions. Their CLOSURE function corresponds to “taking the \(\epsilon\)-closure while also eliminating states unreachable from the start state” in the NFA-to-DFA conversion, and their GOTO function corresponds to the transition function of the final DFA.Show that the language of the following grammar is in LR(0).
E → E + T
E → T
T → (E)
T → idShow that the language of the following grammar is not in LR(0).
E → E + T
E → T
T → (E)
T → id
T → id[E]Algorithm for constructing an SLR(1) table:
1. Construct the collection of sets of LR(0) items for G'.
2. Determine parsing actions for each state Ii as follows:
(a) If a is a terminal and [A → α●aβ] is in Ii,
and GOTO(Ii,a) = Ij, then set ACTION[i,a] to "shift j".
(b) If A is a nonterminal different from S' and if [A → α●]
is in Ii, then set ACTION[i,a] to "reduce A → α" for all
a ∈ FOLLOW(A).
(c) If [S' → S●] is in Ii, then set ACTION[i,$] to "accept".
3. For all nonterminal A, if GOTO(Ii,A) = Ij, set GOTO[i,A] to j.
4. All entries not defined by rule (2) and (3) above are "error".
5. The initial state of the parser is the one constructed from
the set of items containing [S' → ●S].If any conflicting actions result from rule 2, that gives a proof that the grammar is not in SLR(1).
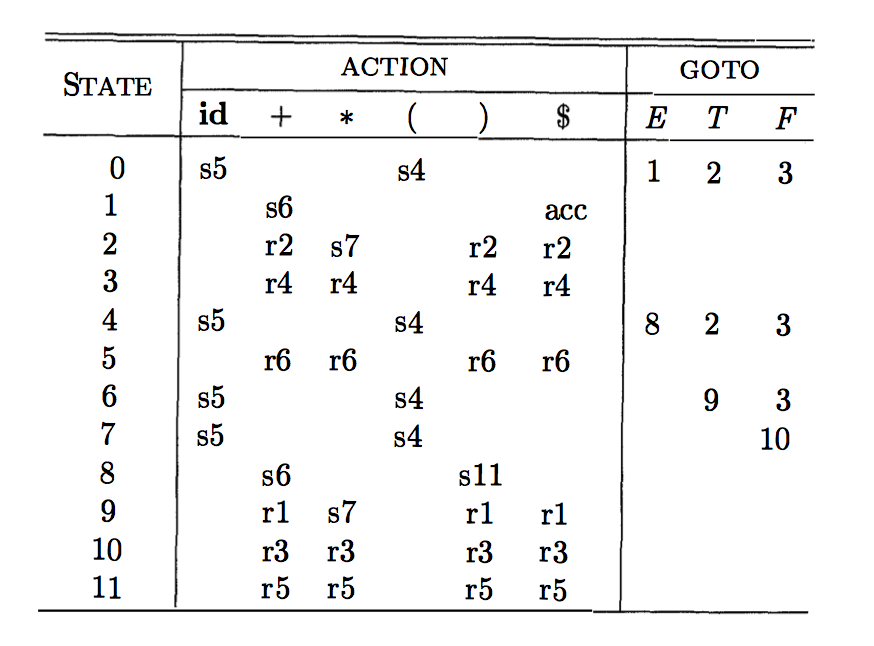
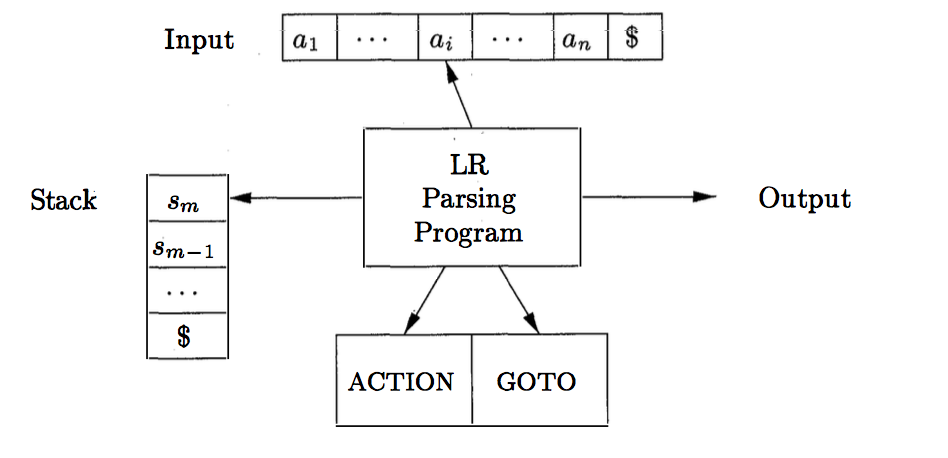
ACTION table, and a GOTO table. All LR parsers have the same architecture and uses the same driver program. They differ only in how they construct their tables.ACTION[i, a], where i is a state and a is a grammar symbol, can have one of four forms:
j, written sj, tells the parser to shift state j onto the stack.j, written rj, tells the parser to reduce by production j, i.e., popping off as many states on the stack as there are symbols on the body of production j, exposing state i on the stack. The parser then pushes onto to the stack the state determined by GOTO[i, A] where A is the head of production j.acc, tells the parser to accept the input and finish parsing.