Poincare Model of Hyperbolic Geometry
The second project in Chapter 1 involves using geometry software to construct the non-Euclidean geometry called 'Hyperbolic Geometry.' To begin, start up GeoGebra. We will use a special file to study Hyperbolic geometry in GeoGebra. This is the file PoincareModel.ggb . Click this link and download the file to your computer. Then, open it using GeoGebra. You will see a screen with a large circle and a Tool Bar having three new Buttons with wrench icons. These are custom tools built for the hyperbolic geometry model. (You may wish to resize the window to see the whole circle. To do this use the tools located under the Move button .)

The first wrench Button has sub-menus for creating basic elements such as lines, rays, segments, and circles. This button also includes measurement of angles and distance. Points are created as usual using the Point Button. The second wrench includes basic constructions including midpoints, perpendiculars, and angle bisectors. The third wrench is a tool to find the intersection of two lines in this geometry. As an example, click on the first wrench and select the line sub-menu. Click twice in the circle to create a hyperbolic line. Note that this line does not look like a 'normal' Euclidean line. That is because it is not Euclidean!

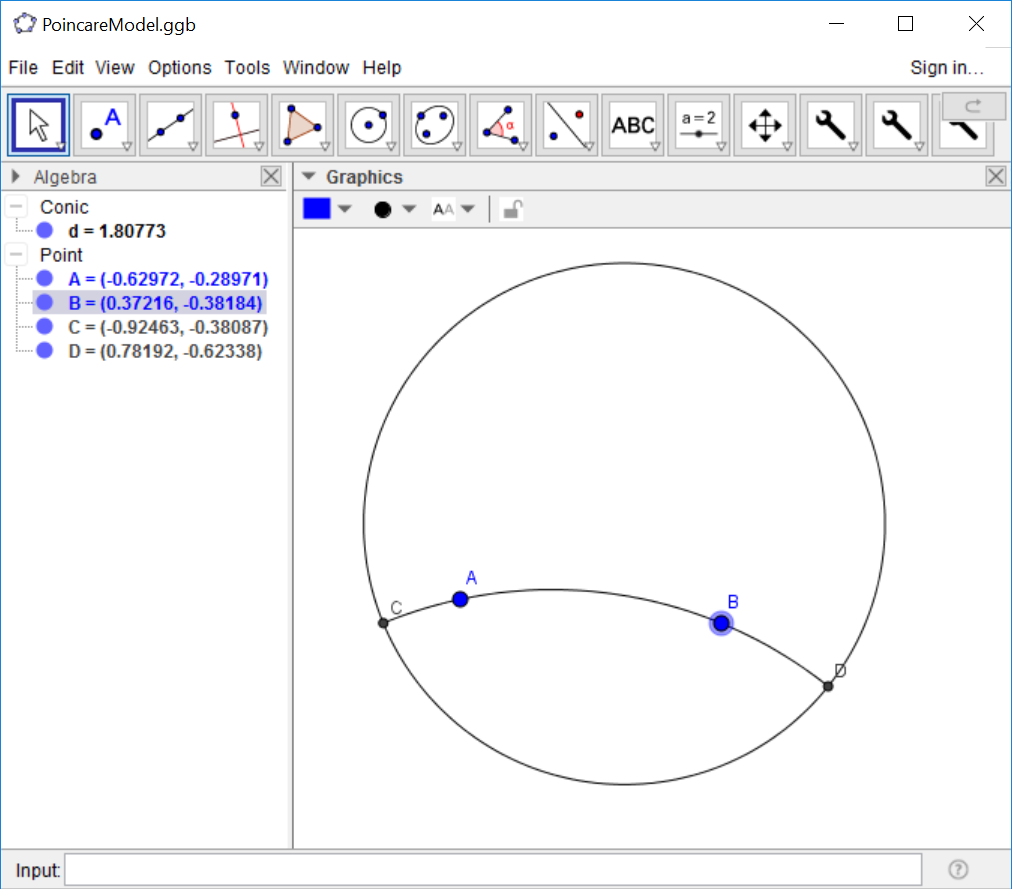
Hyperbolic Segments
On page 45 of the text we discuss what happens to B as we move towards the circle. If this software model were ideal, the point B would never leave the interior of the circle. The points in this geometry are constrained to exist only inside the disk. We do see that the line does not leave the disk, which is accurate. You will have to imagine that point B also cannot leave the disk.

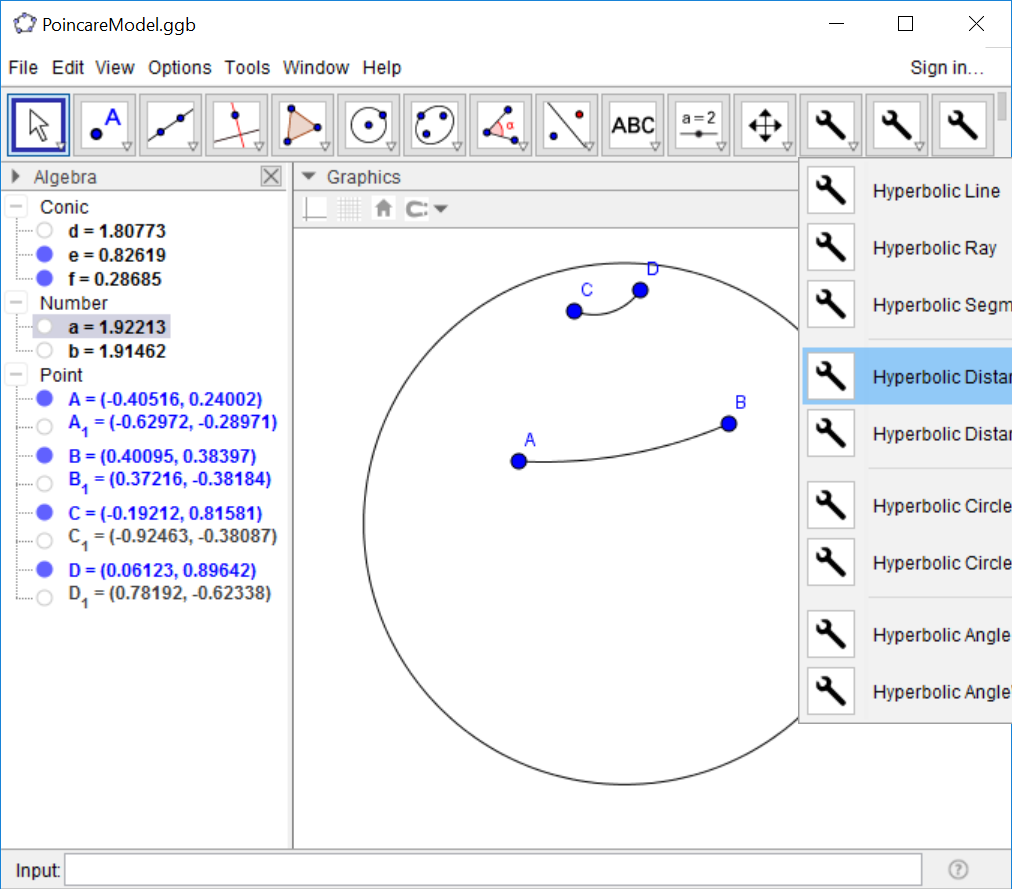
Hyperbolic Length
On page 45 we also discuss what happens to the length of a segment as it is moved around in this hyperbolic geometry. Construct a segment AB near the center of screen. We can measure the length of the segment by selecting the 'Hyperbolic Distance" item under the first wrench button. Then, click on A and B and the numeric result 'a' will appear in the Algebra View. The value of a is the hyperbolic distance from A to B. Next construct hyperbolic segment CD near the edge and measure the hyperbolic distance from C to D. If we adjust C we can make this second distance match the length of AB, although the two 'segments' look very different!

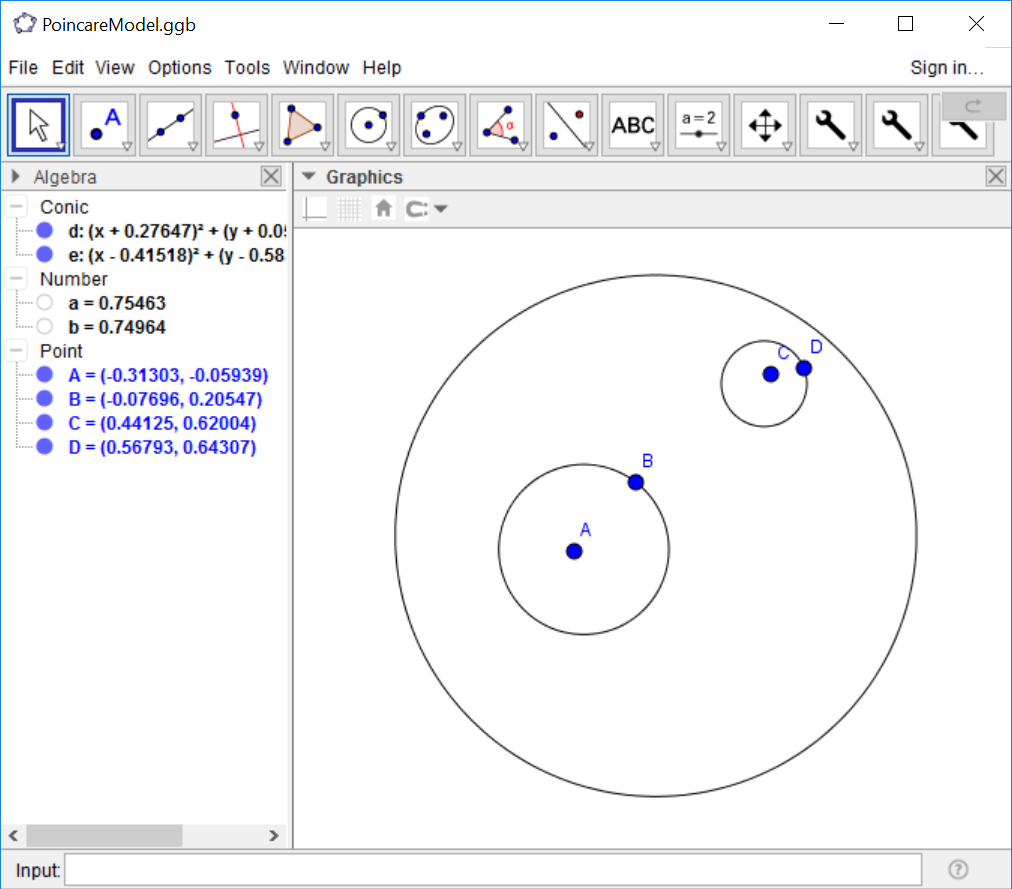
Hyperbolic Circles
On page 46, we create circles in this geometry and notice that circles of different apparent sizes can have the same hyperbolic radii. We can use the Hyperbolic circle tool and the Hyperbolic distance to create circles with this property.

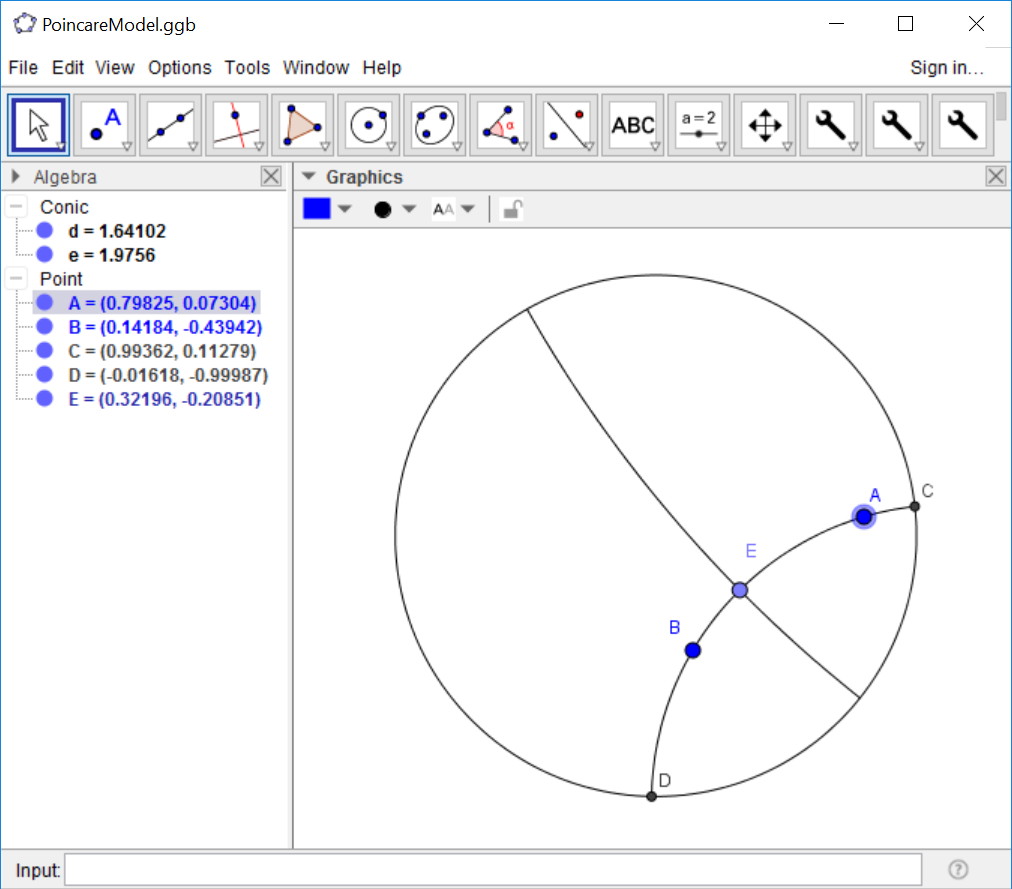
Hyperbolic Angles
On page 47, we look at what happens to angles as we move them via hyperbolic motions. Since movement of points in the GeoGebra model we are using is not really hyperbolic, we can simulate this by looking at what happens to a right angle. Construct a hyperbolic line through A and B. Attach a point E to this line. Choose the 'Hyperbolic Perpendicular at Point" tool under the second wrench button. Click on E and then B to construct the perpendicular. If we move point A or B, we see that that the constructed line remains perpendicular.