Mondrian Art

Start: 10/25/2018
Due: 10/31/2018, by the beginning of class
Collaboration: individual
Important Links: style guidelines, skeleton file (SVG version), skeleton file (StdDraw version), gradesheet

This assignment was designed by Ben Stephenson, University of Calgary. Original language was Haskell.

---

Overview

Piet Mondrian (1872-1944) was a Dutch painter regarded as one of the greatest artists of the 20th century. He was a pioneer in abstract art and created numerous paintings using only simple geometric elements. Some examples of his work are

The site http://www.piet-mondrian.org/paintings.jsp contains a collection of his paintings.

In this project you will write a program to generate art in the Mondrian style. Your program’s output can be either one of the followings:

1. an HTML document containing rectangle primitives within an SVG tag
2. an image drawn by StdDraw on your computer screen

I’m providing two skeleton programs in Kotlin for you to use as a starting point. You should choose either the SVG version or the StdDraw version.

Side Notes:

1. We will go over basic html and the SVG tag in class. If you want to go deeper into SVG, you can read the nice tutorial on SVG here.
2. If you feel like it, you can do both output methods, one program per method, or even one program that does both methods together!

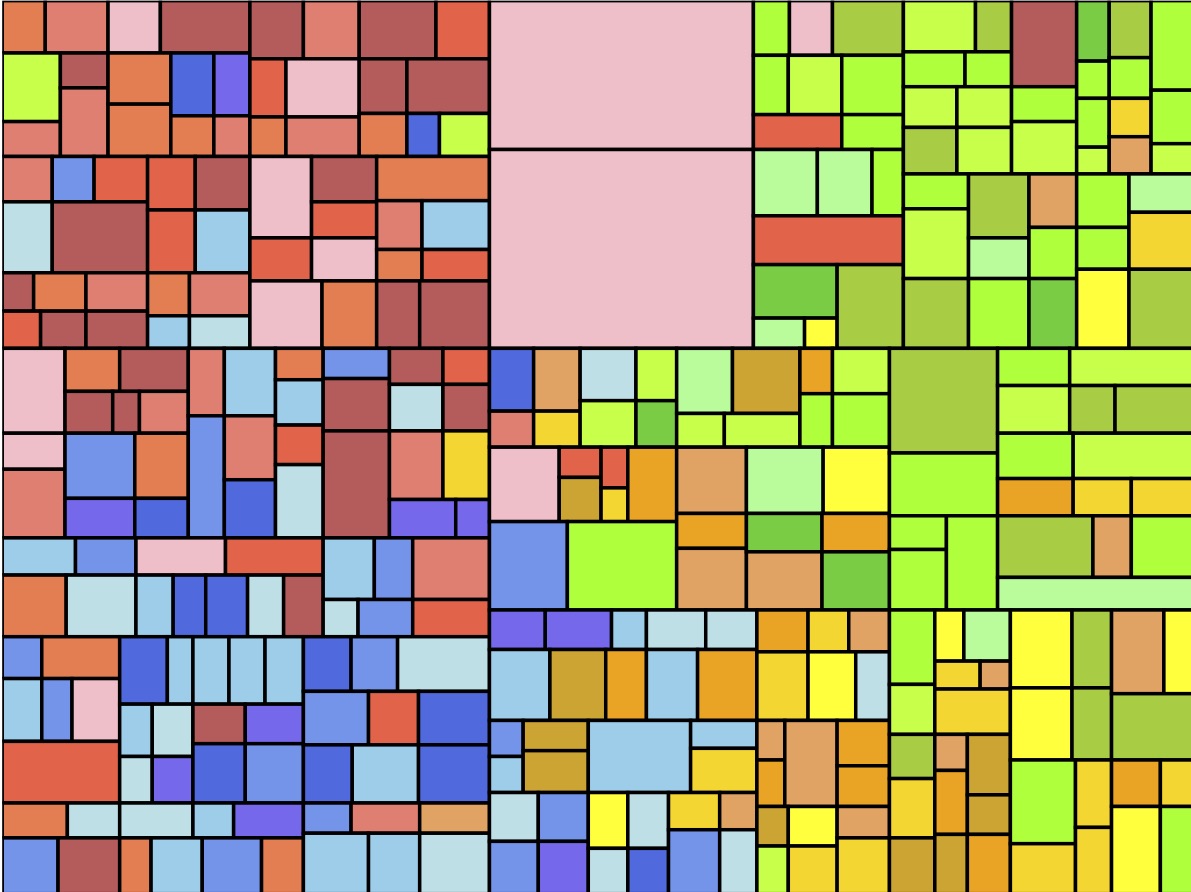
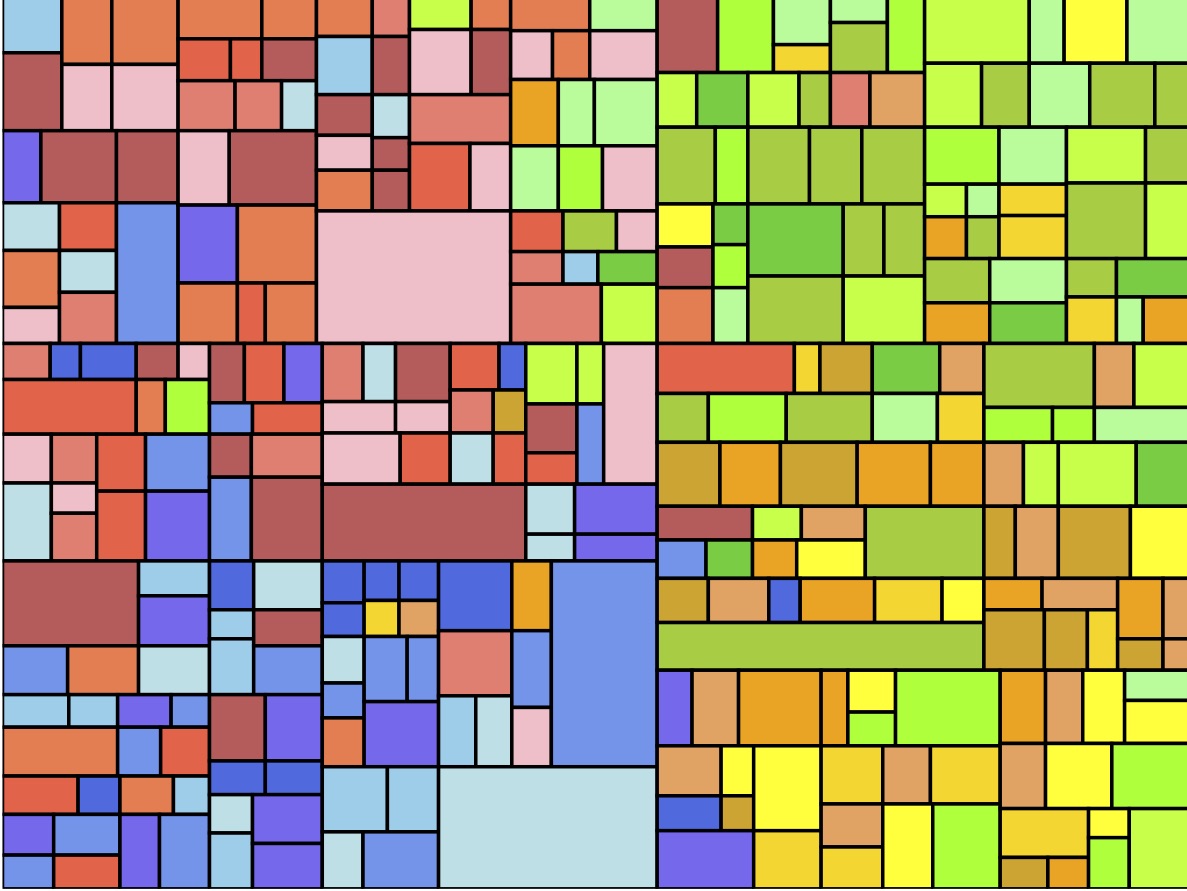
Your task is to modify the recursive mondrian function and add other recursive helper functions to make it generate pseudo-random art in the Mondrian style. As given, the mondrian function simply draws a filled rectangle with a random color and a black outline. You should compile and run the skeleton program to make sure you understand how it works.

Specific tasks

The high-level algorithm for generating a mondrian art should work like this. Given a rectangle (to be called “region” from now on), we decide to do exactly one of the following things.

1. Split the region into 4 smaller regions using a horizontal line and a vertical line. Recurse on each subregion.
2. Split the region into 2 smaller regions of equal height, positioned side by side. Recurse on each subregion.
3. Split the region into 2 smaller regions of equal width, one positioned on top of another. Recurse on each subregion.
4. Do no splitting. Just draw the region with black outline and fill it with a random color.

Here is the algorithm in detail. We decide on one of the 4 choices above using the following algorithm:

    Choose choice 1 if
        (the region is wider than half the initial canvas width
         and taller than half the initial canvas height)
            or
        (the region is big enough to be split both horizontally
         and vertically and was chosen to be split, with a
         probability of 2/3 along each dimension)
    Choose choice 2 if
        (choice 1 does not apply)
           and
        (the region is wider than half the initial canvas width
            or
        the region is wide enough to be split horizontally
        and was chosen to be split, with a probability of 2/3)
    Choose choice 3 if
        (choice 1 and 2 do not apply)
            and
        (the region is taller than half the initial canvas height
            or
        the region is tall enough to be split vertically
        and was chosen to be split, with a probability of 2/3)
    Choose choice 4 if
        none of the above choices 1, 2, or 3 applies

The word “big enough” in the algorithm above can be arbitrarily defined to be, say, at least 120 units.

Once a decision has been made on splitting, we proceed like this.

    If we decide to split into 4 regions:
        choose a random vertical line intersecting the middle one-third
        of the width of the rectangle;
        choose a random horizontal line intersecting the middle one-third
        of the height of the rectangle;
        split the region into 4 smaller regions along the chosen lines;
        recursively call the mondrian function on each subregion;
    else if we decide to split into 2 side-by-side regions:
        choose a random vertical line intersecting the middle one-third
        of the width of the rectangle;
        split the region into 2 smaller regions along the chosen line;
        recursively call the mondrian function on each subregion;
    else if we decide to split into 2 regions, one on top of another:
        choose a random horizontal line intersecting the middle one-third
        of the height of the rectangle;
        split the region into 2 smaller regions along the chosen line;
        recursively call the mondrian function on each subregion;
    else:
        fill the current region (randomly, either white or colored,
        with white 3 times as likely as colored, and if colored,
        with a random determination of red, blue or yellow);

An image generated using this algorithm is shown below.

Once you have the provided algorithm working, save a copy of your program under a different name. You are then encouraged to adjust/expand/adapt this algorithm to generate art with your own specific style provided that it is still at least vaguely Mondrian in style (meaning that it largely consists of horizontal and vertical lines and colored regions, at least the majority of which are rectangular). Ideas for customizing your work that you might want to consider include:

• Using lines of variable width
• Using a broader color palette than red, yellow and blue for the filled regions
• Changing the distribution of random numbers used when selecting the sizes of regions, colors (or anything else random). For example:
  • Instead of using numbers that are an even random distribution, you could add two random numbers together and divide by two to form a distribution that favors numbers in the middle of the random space.
  • Instead of allowing all possible values, reduce the space to numbers that are evenly divisible by 10 (or 20 or some other number) so that the random lines have more regular spacing to them.
  • Using a patterned fill for some regions instead of only using solid fills
  • Occasionally splitting a region into something other than rectangles
  • Occasionally split a region into 3 smaller regions instead of 2 or 4

For inspiration, here are a couple of other images that I generated with different variations of my solution. In both of these images, the color used to fill the region is influenced (but not fully determined) by its location:

Gradesheet

We will use this gradesheet when grading your lab.

Submission

You must implement the basic algorithm described in this document and save and submit a version of your code that implements the basic algorithm. Then you are free to go on to modify/extend your program to demonstrate your artistic talents. Failure to submit a version of the program that implements the provided algorithm will cause us to assume that any difference occurred because you weren’t able to implement the algorithm correctly rather than due to artistic choice.

Note: Since the results from your program are random, you may also want to submit a few html or image files for your favorite images that your program has generated since we will probably not see the same images when we test your program.

Submit your .kt file (or files if you attempt the A/A+ part). See gradesheet. Zip up your files (if submitting more than 1 file) and submit via Moodle.

Powered by pandoc and hakyll.